از حل کننده در اکسل استفاده کنید تا تعداد واحدهایی را از هر کارخانه به هر مشتری ارسال کنید که کل هزینه را به حداقل می رساند.
دانلود فایل اکسل این آموزش transportation-problem
فرمول بندی مدل
مدل اکسل ما به صورت زیر در نظر گرفته شده است.
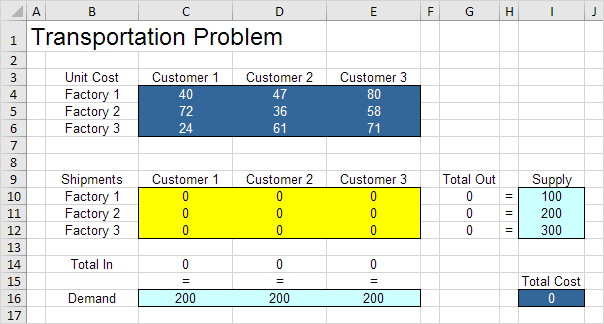
1. برای فرموله کردن مسئله حمل و نقل، به سه سوال زیر پاسخ دهید.
a. تصمیمات اتخاذ می شود؟ برای این مشکل، ما نیاز به اکسل برای پیدا کردن چند واحد از هر کارخانه به هر مشتری حمل می شود.
b. محدودیت های این تصمیمات چیست؟ هر کارخانه دارای عرضه ثابت است و هر مشتری تقاضای ثابت دارد.
c. اندازه گیری کلی عملکرد برای این تصمیمات چیست؟ اندازه گیری کلی عملکرد کل هزینه حمل و نقل است، بنابراین هدف این است که این مقدار را به حداقل برسانیم.
2. برای ایجاد مدل ساده تر، می توانید محدوده های زیر را نام ببرید.
| نام محدوده | سلول ها |
|---|---|
| UnitCost | C4:E6 |
| Shipments | C10:E12 |
| TotalIn | C14:E14 |
| Demand | C16:E16 |
| TotalOut | G10:G12 |
| Supply | I10:I12 |
| TotalCost | I16 |
3. توابع زیر را وارد کنید.
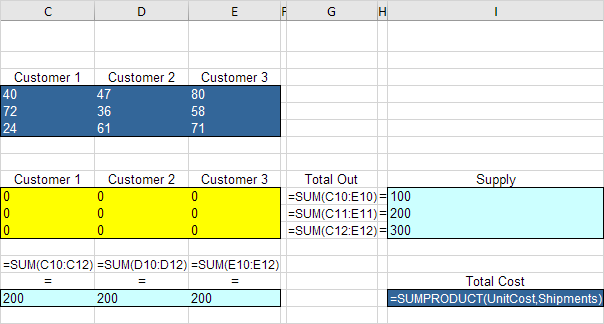
توضیح: توابع SUM کل جمع آوری شده از هر کارخانه (Total Out) را به هر مشتری (Total In) حمل می کند. کل هزینه برابر با sumproduct از UnitCost و ارسال محموله های.
آزمون و خطا
با استفاده از این فرمولاسیون، هر راه حل محاکمه ای آسان می شود.
برای مثال، اگر ما 100 واحد از کارخانه 1 به مشتری 1، 200 واحد از کارخانه 2 به مشتری 2، 100 واحد از کارخانه 3 به مشتری 1 و 200 واحد از کارخانه 3 به مشتری 3، مجموع از برابر به عرضه و مجموع در برابر تقاضا این راه حل مجموع هزینه 27800 است.
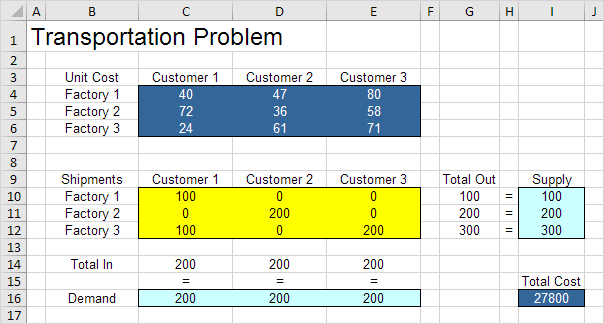
استفاده از آزمایش و خطا لازم نیست. ما بعدا توضیح خواهیم داد که چگونه می توان از حلال اکسل برای یافتن راه حل بهینه استفاده کرد.
مدل را حل کنید
برای پیدا کردن راه حل بهینه، مراحل زیر را اجرا کنید.
1. در بخش داده، در گروه آنالیز، روی Solver کلیک کنید.
توجه: دکمه حل کننده را نمی توان پیدا کرد؟ برای بارگیری افزونه Solver اینجا را کلیک کنید .
پارامترهای حل کننده را وارد کنید (به عنوان خوانده شده). نتیجه باید با تصویر زیر سازگار باشد.
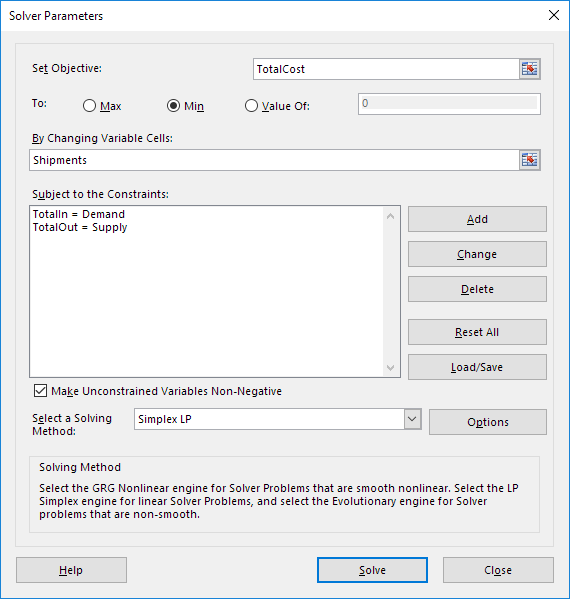
شما انتخاب تایپ کردن نام دامنه یا کلیک روی سلولهای صفحه گسترده را دارید.
2. TotalCost را برای هدف وارد کنید.
3. روی Min کلیک کنید.
4. حملات را برای تغییر سلول های متغیر وارد کنید.
5. برای وارد کردن محدودیت زیر، روی افزودن کلیک کنید.
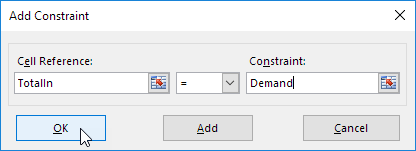
6. برای وارد کردن محدودیت زیر، روی افزودن کلیک کنید.
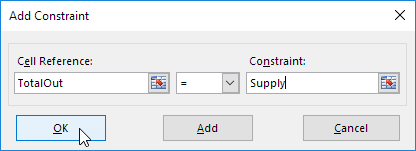
7. بررسی کنید “متغیرهای بدون محدودیت غیر منفی” را انتخاب کنید و Simplex LP را انتخاب کنید.
8. در نهایت، روی حل کلیک کلیک کنید.
نتیجه:
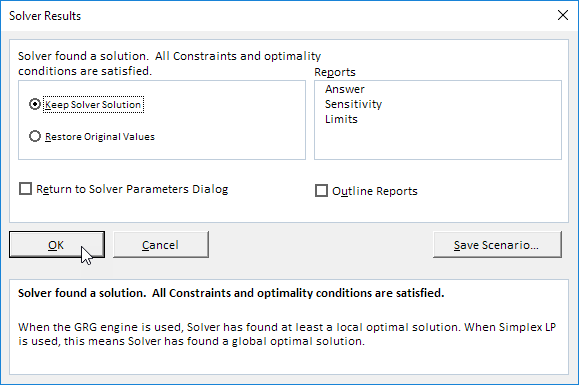
راه حل بهینه:
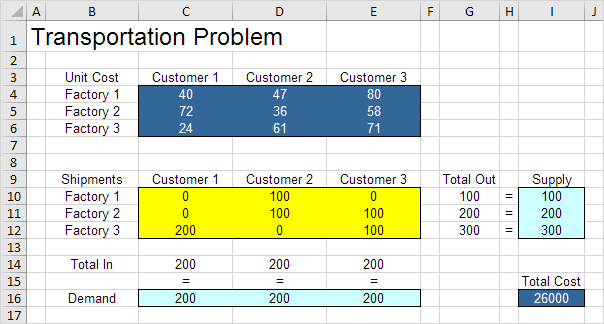
نتيجه گيري: بهينه سازي 100 واحد از کارخانه 1 به مشتري 2، 100 واحد از کارخانه 2 به مشتري 2، 100 واحد از کارخانه 2 به مشتري 3، 200 واحد از کارخانه 3 به مشتري 1 و 100 واحد از کارخانه 3 به مشتري 3. این راه حل حداقل هزینه 26000 را می دهد. تمام محدودیت ها راضی هستند.
 آموزش رایگان آموزی بزرگترین مرجع آموزشی رایگان
آموزش رایگان آموزی بزرگترین مرجع آموزشی رایگان
