فرمول آماری آزمون Z چیست؟
آزمون Z یک روش آماری است که برای آزمایش فرضیه جایگزین در برابر فرضیه تهی استفاده می شود. آزمون Z تعیین می کند که آیا بین نمونه و میانگین جمعیت تفاوت معنی داری وجود دارد یا خیر. Z تست به طور معمول برای مقابله با مشکلات مربوط به نمونه های بزرگ استفاده می شود. نام “تست” درایو از آن دخالت از توزیع استاندارد عادی ساخته شده است و “Z” نمادی سنتی است که برای نشان دادن متغیر تصادفی عادی استاندارد استفاده می شود. وقتی اندازه نمونه بیش از 30 واحد باشد در این حالت باید آزمایش z انجام شود. فرمول تست z به به صورت زیر است،
در اینجا،
- x̄ = میانگین نمونه
- μ = میانگین جمعیت
- σ = انحراف معیار جمعیت
- n = تعداد مشاهده
نمونه هایی از فرمول آماری تست Z (با مثال Excel)
بیایید مثالی بزنیم تا محاسبه فرمول آمار آزمون Z را به شیوه ای بهتر درک کنیم.
فرمول آمار آزمون Z – مثال # 1
فرض کنید شخصی می خواهد چای و قهوه هر دو در شهر به همان اندازه محبوب باشند یا بررسی کند. در این حالت، او می تواند از روش آماری آزمایشی az استفاده کند تا نتایج را با در نظر گرفتن حجم نمونه مثلاً 500 نفر از شهر دریافت کند که فرض کنید 280 نفر از آنها نوشیدن چای هستند. بنابراین برای آزمایش این فرضیه می توان از روش z test استفاده کرد.
مدیر مدرسه در مدرسه ادعا می کند که دانش آموزان در مدرسه او بالاتر از هوش متوسط و نمونه تصادفی از 30 دانش آموز IQ نمره متوسط 112.5 و میانگین ضریب هوشی جمعیت 100 با انحراف استاندارد 15 است. آیا شواهد کافی برای حمایت از ادعای اصلی وجود دارد ؟
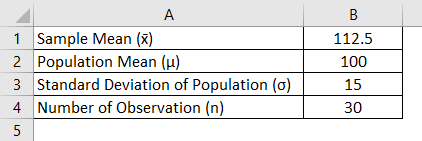
راه حل:
آمار آزمون Z با استفاده از فرمول مندرج در زیر محاسبه می شود
(Z Test = ( x̄ – μ) / ( σ / √n
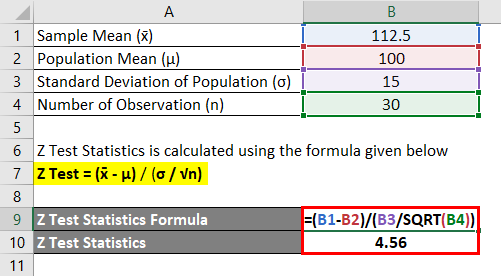
- تست Z = (112.5 – 100) / (15 / √30)
- تست Z = 4.56
نتایج آزمون z را با جدول استاندارد z مقایسه کنید و می توانید در این مثال نتیجه بگیرید که فرضیه تهی رد شده و ادعای اصلی درست است.
فرمول آمار آزمون Z – مثال شماره 2
فرض کنید یک سرمایه گذار که به دنبال تجزیه و تحلیل میانگین بازده روزانه سهام یکی از شرکت است از 1٪ بیشتر است یا خیر؟ بنابراین سرمایه گذاران نمونه تصادفی 50 را برداشت و بازده محاسبه می شود و میانگین آن 0.02 است و سرمایه گذاران در نظر گرفته شده که انحراف استاندارد میانگین 0.025 است.
بنابراین، در این حالت، فرضیه تهی است که میانگین 3٪ و فرضیه جایگزین آن است که میانگین بازده بالاتر از 3٪ است. سرمایه گذاران فرض می کنند که آلفای 0.05٪ به عنوان یک تست دو دم و 0.025٪ نمونه در هر دم انتخاب شده و مقدار بحرانی آلفای آن 1.96 یا 1.96 است. بنابراین اگر نتیجه آزمایش Z کمتر یا بیشتر از 1.96 فرضیه تهی رد شود.
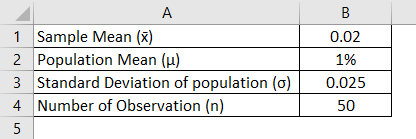
راه حل:
آمار آزمون Z با استفاده از فرمول مندرج در زیر محاسبه می شود
(Z Test = ( x̄ – μ) / ( σ / √n
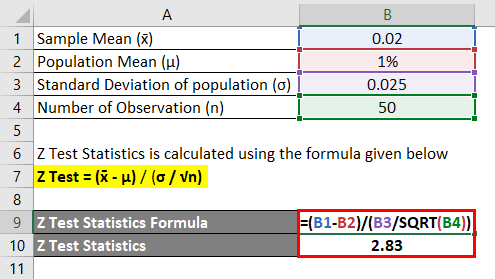
- تست Z = (0.02 – 1٪) / (0.025 / √50)
- تست Z = 2.83
بنابراین از محاسبه فوق سرمایه گذاران نتیجه می گیرند و او فرضیه تهی را رد می کند زیرا نتیجه z از 1.96 بیشتر است و به تجزیه و تحلیل می رسند که میانگین بازده روزانه سهام بیش از 1٪ است.
فرمول آمار آزمون Z – مثال شماره 3
یک شرکت بیمه در حال حاضر در حال بررسی نرخ های سیاست فعلی خود است که در ابتدا نرخی را تعیین می کند که معتقدند میانگین مبلغ ادعا حداکثر 180000 روپیه خواهد بود. این شرکت نگران این میانگین واقعی است که در واقع بالاتر از این است. شركت به طور تصادفي 40 ادعاي نمونه را انتخاب كرده و ميانگين نمونه 195000 روپيه را محاسبه مي كند با فرض انحراف استاندارد از ادعا 50000 روپيه و آلفا را 0.05 تعيين مي كند. بنابراین تست z که برای دیدن شرکت بیمه باید انجام شود نگرانی دارد یا خیر.
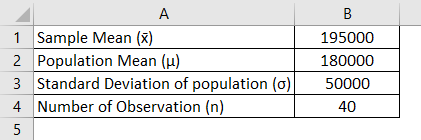
راه حل:
آمار آزمون Z با استفاده از فرمول مندرج در زیر محاسبه می شود
(Z Test = ( x̄ – μ) / ( σ / √n
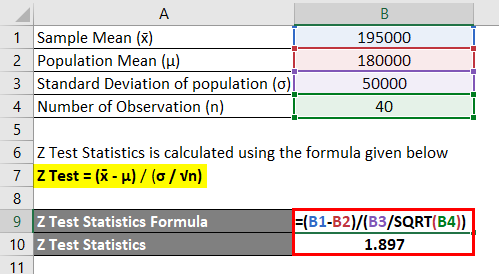
- Z Test = (195000 – 180000) / (50000 / √40)
- تست Z = 1.897
مرحله – 1 فرضیه Null را تنظیم کنید
مرحله – 2 آمار آزمون را محاسبه کنید
بنابراین اگر تمام ارقام موجود را در فرمول تست z قرار دهید، نتایج آزمون z را برابر با 1.897 می دهد
مرحله – 3 منطقه رد را تنظیم کنید
با توجه به آلفای 0.05، بیایید بگوییم که منطقه رد 1.65 است
مرحله – 4 نتیجه گیری
طبق نتایج آزمون z، می توانیم ببینیم که 1.897 از منطقه رد 1.65 بیشتر است بنابراین شرکت نتواند فرضیه تهی را نپذیرد و شرکت بیمه باید نگران سیاستهای فعلی خود باشد.
توضیح
- ابتدا میانگین نمونه را تعیین کنید (میانگین وزنی کل نمونه های تصادفی است).
- میانگین میانگین جمعیت را تعیین کنید و میانگین میانگین نمونه را از آن جدا کنید.
- سپس مقدار حاصل را با انحراف استاندارد تقسیم بر ریشه مربع تعدادی از مشاهدات تقسیم کنید.
- پس از انجام مراحل فوق، نتایج آزمون z محاسبه می شود.
ارتباط و استفاده از فرمول آماری آزمون Z
از آزمون Z برای مقایسه میانگین یک متغیر تصادفی عادی با یک مقدار مشخص استفاده می شود. آزمون Z مفید است یا در صورت استفاده از نمونه بیش از 30 و واریانس جمعیت شناخته شده است. آزمون Z بهتر است با این فرض که توزیع میانگین نمونه طبیعی است. در صورت ایجاد شرایط خاص، از آزمایش Z استفاده می شود، در غیر این صورت مجبور به استفاده از تست های دیگر هستیم و نوسانات در تست z وجود ندارد. از آزمون Z برای یک وسیله واحد برای آزمایش فرضیه ارزش ویژه میانگین جمعیت استفاده می شود. آزمون Z یکی از پایه های روشهای تست فرضیه آماری است و اغلب در سطح مقدماتی یاد می گیرد. بعضی از زمانهای آزمایش z می توانند در جایی که داده ها از توزیع دیگر مانند Binomial و Poisson تولید می شوند، استفاده شوند.
 آموزش رایگان آموزی بزرگترین مرجع آموزشی رایگان
آموزش رایگان آموزی بزرگترین مرجع آموزشی رایگان
